Syfte och lärandeobjekt
Syftet med lektionen är att tillsammans undersöka och bygga vidare på hur man med idén om n som en enhet i ett mönster kan skriva uttryck för mönster med icke-konstant ökning. Vidare är syftet också att tillsammans komma till insikt att mönster kan omgrupperas, utan att talföljden påverkas, som ett verktyg för att enklare identifiera n i ett mönster och på så sätt skriva ett algebraiskt uttryck.
Material
Ett fungerande lärarkonto på socrative med quizen för Lektion 3 importerad.
https://b.socrative.com/teacher/#import-quiz/34863076
Se länk för instruktion om hur man importerar och startar en quiz i socrative.
Lektionsbeskrivning
Ni kommer att arbeta med en undersökande aktivitet i en geogebra-applet som innehåller en uppställning av hexagonaltalen ( 2n2 – n ). Eleverna ska bekanta sig med regeln som mönstret ökar med för att slutligen, genom att om-arrangera varje figur till rektanglar, skapa ett generellt uttryck för talföljden. Aktiviteten sekvenseras med hjälp av frågor i socrative som underlag för ett undersökande samtal i matematik i helklass.
Introduktion
Förslag på formuleringar för att inleda lektionen:
Vi ska idag knyta ihop arbetet med mönster som varit i fokus de senaste lektionerna. Idag ska vi arbeta med ett annorlunda, mer utmanande mönster. (Visa nu de första två figurerna i hexagonaltal-appleten) Hur många prickar förväntar ni er i figur 3? (när eleverna gissat, så klickar du fram figur 3)
Detta är som sagt ett lite mer utmanande mönster, men visst vore det spännande att kunna ta reda på hur många prickar det blir i figur 1000?
Aktivitet
- Kopiera länken och klistra in i ett nytt fönster. Använd appleten och försök att bygga figur 4. https://www.geogebra.org/m/vH6DkjxW
Hur många prickar har figur 4 totalt?
- 25
- 24
- 28
- 32
- Inget av ovanstående
- Vet ej
Vad?
Eleverna ska förstå hur mönstret byggs upp och talföljden utvecklas
Hur?
Eleverna undersöker mönstret parvis, någon elev får sedan visa figur 4 på lärardatorn och berätta hur hen tänkte.
Gör återkoppling till lektion 2, att det ibland är svårt att finna uttryck för mönster, men minns att ni lyckades med kvadraten (kvadrattalen) i förra lektionen. Visa appleten som har både kvadrattalen och hexagonaltalen (https://www.geogebra.org/m/V7cwYH2u). Diskutera hur ni gjorde för att få fram uttrycket till kvadrattalen (basen*höjden). Diskutera också hur regeln för ökningen liknar varandra mellan kvadrattalen och hexagonaltalen och att ni kommer behöva tänka lite nytt även här. Försök att inte fastna i för mycket detaljer kring ökningen och ökningens ökning i de båda mönstren, konstatera istället att det verkar finnas likheter.
Varför?
Vi har sett att det är viktigt att eleverna redan inledningsvis känner sig förtrogna med mönstrets regelbundenhet.
Vi har sett att vi behöver hjälpa eleverna med återkoppling till liknande problem vi stött på tidigare. Basen*höjden kommer ni att behöva använda när mönstret väl har strukturerats om till rektanglar. Det blir verktyget för att skriva uttrycket, men också motivet till varför det vore fruktbart att arrangera om prickarna i mönstret.
- Visst vore det bra om varje figur i vårt mönster hade en form så vi kunde använda ”basen*höjden”? https://www.geogebra.org/m/vH6DkjxW
Går det?
- Ja
- Nej
- Det beror på
Vad?
Utmana normen och elevernas uppfattning om att mönstret ej får manipuleras och transformeras.
Hur?
Eleverna undersöker parvis hur de kan arrangera om prickarna i varje figur i appleten. Någon elev får sedan visa på figur 2 och 3 hur hen gjort på lärardatorn. Här finns också utrymme för resterande klass att ställa frågor till eleven vid lärardatorn.
Du letar efter en elev som skapat någon typ av kvadrat och/eller rektangel som har en sida som är n prickar lång. Var också med på att någon elev antagligen kommer att försöka lägga prickarna över varandra. Påpeka då att det förändrar mer än bara bilden av mönstret, det förändrar även talföljden vilket skulle göra att det blir ett annat uttryck.
Varför?
Ni behöver någon figur där ni kan börja leta enheter, så som ni gjorde i lektion 1 och 2. Eleverna behöver också få veta att det är ok att förändra hur ett mönster ser ut, så länge de inte ändrar själva talföljden. Ett mönster som ser väldigt avancerat ut kan ibland arrangeras om till något mer hanterbart.
- Pröva att hitta n*n i varje figur i vårt mönster. https://www.geogebra.org/m/vH6DkjxW
Går det?
Vad?
Använda verktyg från föregående lektioner, så som att se enheten n i ett mönsters struktur och att använda sig av basen*höjden, i nya sammanhang.
Hur?
Eleverna utgår ifrån de transformerade figurerna i fråga 2 och undersöker parvis hur man kan hitta n i figuren och använda basen*höjden.
Om det finns flera olika lösningar, låt dessa komma fram till tavlan och markera med en penna hur de tänkte. Ge utrymme för eleverna att ställa frågor till varandra.
Be eleverna att i paren komma fram till ett sätt att även skriva ett uttryck för den rektangel som blir över när ni hittat n*n. Låt eleverna återigen få visa sina resonemang genom att ringa in och skriva på tavlan. Påpeka sedan att ni nu kan lägga ihop de två uttrycken för att få ett uttryck som beskriver hela figuren.
Om det finns tid kvar av lektionen, och lösningen inte redan dykt upp, presentera den fiktiva elevlösningen n(2n-1) och be dem fundera över hur denna elev har resonerat. Lyft sedan eleverna förslag till en helklassdiskussion.
Om någon elev kommit fram till en intressant lösning på egen hand, låt denna presentera vid tavlan och säg sedan till klassen ”om 3min så ska ni antingen kunna återberätta hur Sabina har tänkt, annars så ska ni har en fråga till Sabina som gör att ni förstår det bättre” för att stimulera till undersökande samtal i matematik.
Varför?
Beroende på omständigheter i klassrummet och hur långt eleverna kommit i sin matematikutveckling så behövs det viss stöttning. Här hjälper du eleverna att bryta ner problemet till något som är mer likt det de jobbat med tidigare, men utmanar dem samtidigt.
Den fiktiva elevlösningen ska stimulera till undersökande samtal kring ett alternativt tillvägagångssätt men som också ger samma svar. Vi har sett att denna lösning ibland kommer upp spontant i klassrummet och har då skapat intressanta samtal.
Uppmaningen om att eleverna ska kunna återberätta, alternativt formulera en fråga utmanar eleverna att tänka till kring en annan elevs resonemang. Den har potential att skapa ett mer undersökande klassrumsklimat där eleverna förväntas ställa frågor till varandra och kunna både förklara sitt eget resonemang och sätta sig in i någon annans.
- Testa om uttrycket stämmer!
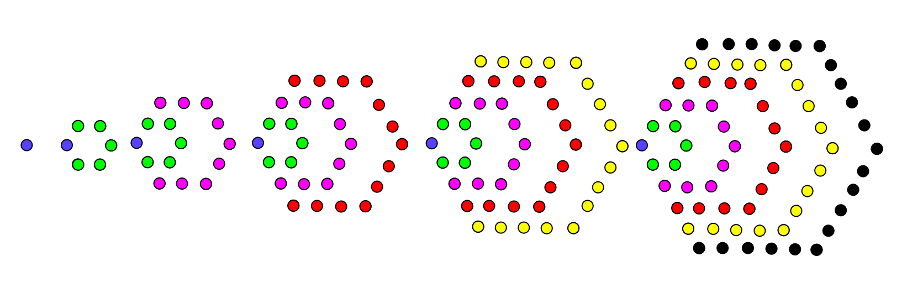
Vad?
Eleverna ska bekräfta att det nya verktyget att transformera ett mönster innan de tar fram ett uttryck faktiskt fungerar.
Hur?
Eleverna testar uttrycket, enskilt eller i par, på valfri figur 1-6 och har sedan möjlighet att kontrollräkna prickarna i bilden.
Om du har en elev som du misstänker kommer tycka att uppgiften är meningslös och som behöver en större utmaning, be denne att istället beräkna antalet prickar i figur 1000 i enlighet med premissen för lektionen. Annars kan ni göra det tillsammans som en avslutning på lektionen.
Varför?
Vi vet att uppgiften är krävande, och att delar av klassen kommer att vara mer bidragande till att lektionen går framåt än andra. Sista uppgiften fångar därför upp elever som blivit mer passiva och ger dem en chans att igen bli aktiva. Uppgiften är ändå en utmaning för många, då den kräver förståelse och förtrogenhet att hantera algebraiska uttryck, men faller inte inom ramen för problemlösning på samma sätt som övriga lektionen.
Avslutning
En bra avslutning är att återkoppla till lektion 1 och sammanfatta de viktigaste poängerna sedan dess. Inledningen i lektion 1 handlar om styrkan i matematik och hur vi kan se mönster i vår omvärld som går att beskriva med mönster. Ni har nu tillsammans fått en djupare inblick i hur man kan arbeta med mönsters struktur för att skapa beskrivande algebraiska uttryck. Eleverna har gått ifrån enkla resonemang så som uppräkning från figur ett och framåt (additiva resonemang) till att hitta förändringar och enheter i mönstret (multiplikativa resonemang). Ni har även sett att mönster går att arrangera om (transformativa resonemang) för att skapa figurer som är enklare att beskriva utifrån multiplikativa resonemang för att lösa ett avancerat mönster.
