Lektion 1

Syfte och lärandeobjekt

Syftet med lektionen är att tillsammans undersöka och komma till insikt om betydelsen av n vid skapandet av generella algebraiska uttryck av mönster, och att n kan ses på olika sätt i en sådan process. Speciellt att n kan ses som antalet ökningar (om Figur n = 3n+1 så har Figur 5 ökat med 3 5gånger) eller att n kan ses som enhet i en figurs struktur (att i Figur 5 så går det att hitta enheten 5 3gånger). För vidare förklaring, se den didaktiska vägledningen.

Material

Skapa ett fungerande lärarkonto på socrative där du importerar quizen som heter lektion 1 https://b.socrative.com/teacher/#import-quiz/34963399

Se länk för instruktion om hur man importerar och startar en quiz i socrative.

Lektionsbeskrivning

Ni kommer skapa undersökande samtal i matematik med hjälp av Socrative. Eleverna får diskutera olika fiktiva elevers resonemang om ringmönstret och ta ställning på socrative. Eleverna får även manipulera mönster med hjälp av färgläggning i en applet, som en väg till algebraiska generaliseringar. Mönstren görs tillgängligt för eleverna via en länk, så att de får möjlighet att själva pröva olika färgläggningar som stöd för sina resonemang. Datorn gör det enkelt att ångra, börja om och modifiera deras färgläggning. Återkommande i lektionen är helklassdiskussioner kring olika elevlösningar.

Introduktion

Förslag på formuleringar för att inleda lektionen:

En viktig användning av matematik är för att strukturera och beskriva vår omvärld. Ett exempel är att se samband och mönster i närmiljön, till exempel när det kommer till antalet kronblad hos en blomma. Denna lektion kommer därför att handla om mönster och hur dessa kan beskrivas.
Vi kommer under lektionen undersöka mönster och till vår hjälp kommer ni använda dator, penna och papper. Vi vill att ni tar fram en tom sida att anteckna på om ni skulle behöva eller blir uppmanade att anteckna samt att datorn är igång med enbart en flik öppen i webbläsaren. Ni kommer att få frågor i Socrative och det förväntas att ni motiverar era svar muntligt med ett matematiskt resonemang.
Nu kommer ni få en fråga på Socrative.com. För att hitta den frågan väljer ni student login och rumsnummer ___. Den första frågan ni får tänker ni och svarar på enskilt. Jag kommer att klicka fram nya frågor allt eftersom.

Aktivitet

Uppgifterna nedan stämmer överens med frågorna i den importerade socrative-quizen.

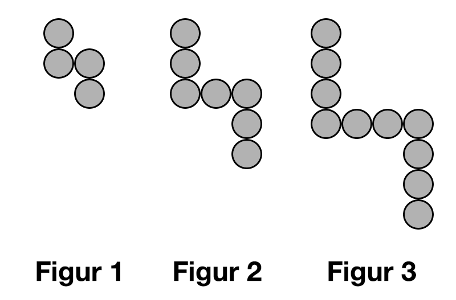
1. Hur många prickar finns i figur 4? (Enskilt)
   1. 12
   2. 13
   3. 14
   4. 15
   5. Vet ej

Vad?

Eleverna ska förstå hur mönstret byggs upp och talföljden utvecklas

Hur?

Eleverna undersöker först enskilt och ni diskuterar sedan i helklass hur de kommer fram till figur nummer 4.

Du kan använda följande frågor för att stimulera elevernas undersökande samtal kring mönstret i helklass:

• Hur kom ni fram till det? Finns det en regel?
• Var det någon som tänkte på ett annat sätt?
• Hur kom ni fram till att ökningen är 3?
• Hur kan vi se ökningen i talen?
• Hur kan vi se ökningen i figuren? Låt elever gå fram och indikera på tavlan, t.ex. med en penna.
• Kan du färglägga de tre nya prickarna i figur 2?

Varför?

Vi har sett att det är viktigt att eleverna redan inledningsvis känner sig förtrogna med mönstrets regelbundenhet.

Med de fördjupande frågorna vill vi att flera olika resonemang presenteras för att skapa förutsättningar för undersökande samtal, särskilt att betydelsen av n som en upprepad ökning kopplas till bilden.

2. Hur många prickar finns i figur 9? (Enskilt)
   1. 30
   2. 28
   3. 27
   4. 25
   5. Vet ej

Vad?

Befästa elevernas förståelse för talföljden och utmana deras metod för att komma fram till antalet prickar i vilken figur som helst.

Hur?

Eleverna löser och svarar på uppgiften enskilt

Ni för ingen uppföljande diskussion om elevernas svar utan visar bara resultatet (How’d we do).

Varför?

Vi vill spara diskussionen om elevernas metoder till efterföljande fråga, dels för att ytterligare kunna utmana elevernas metoder och dels för att spara tid.

3. Baserat på metoden du använde i uppgiften innan, skulle du kunna räkna ut antalet prickar i figur 1000, under en minut? (Enskilt)

Vad?

Utveckla elevers förståelse för olika metoders gångbarhet.

Hur?

Eleverna diskuterar varandras lösningsmetod för att upptäcka deras styrkor och svagheter

Uppmana eleverna att beskriva för sin kamrat hur de kom fram till sitt svar i uppgiften innan. Och motivera varför/varför inte de skulle hinna figur 1000 under en minut. Detta resonemang följs upp i helklassdiskussion.

Varför?

En del av lektionens mål är att eleverna ska inse betydelsen av generella uttryck. Vi vill knyta an till den typen av matematiska problem som beskrevs i inledningen och skapa en drivande fråga för att jobba vidare med metoder för att konstruera generella uttryck. Genom att välja ett exempel som ligger relativt nära (figur 9) och ett exempel långt bort (figur 1000) så kan vi skapa underlag för undersökande samtal kring olika metoders styrkor och svagheter.

4. Om jag ber er att säga hur många prickar som finns i figur n vad tror ni att jag menar då? (Enskilt, sen par, skriv sedan ett svar per par)

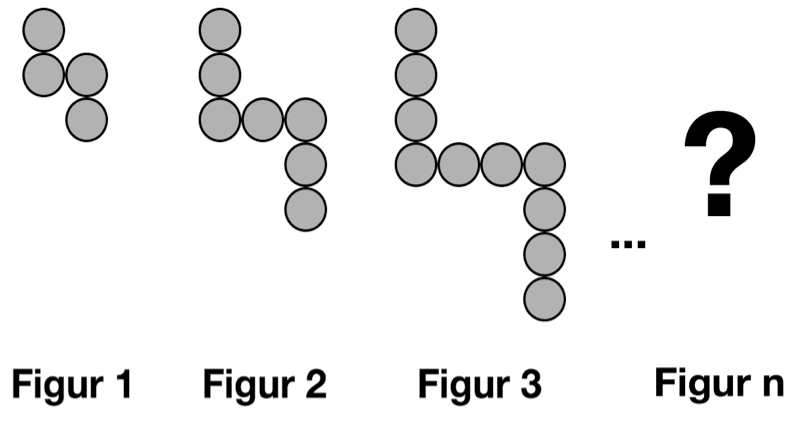
Vad?

Eleverna ska förstå att de kan använda n för att benämna vilken figur som helst

Hur?

Eleverna tänker först själva och diskuterar sedan i par hur de tolkar uttrycket ’Figur n’. När de kommit överens så skriver de sin formulering i Socrative.

Be eleverna att läsa igenom svaren på tavlan och välja det svar, inte deras eget, som de tycker ger bäst svar på frågan. De ska förbereda sig på att motivera sina val. Diskutera sedan i helklass.

Du kan använda följande frågor för att stimulera elevernas undersökande samtal kring tolkningarna i helklass:

• Hur tror ni en grupp som svarat så här tänker?
• En grupp som svarat med ett uttryck, hur tror ni de tänker att kopplingen mellan n i uttrycket är till n i ’Figur n’?

Varför?

Vi har sett att många elever förknippar n med algebraiska uttryck. Vi vill att eleverna ska se n i olika sammanhang, både som en del av ett uttryck och som figurens nummer. Senare uppgifter utmanar elevernas förståelse för vad n står för i ett uttryck och hur det kan kopplas till figurens nummer.

5. Miriam tänkte enligt bilden, välj det uttryck som du tycker passar bäst (alltså ett av dem under) till hennes bild. (Enskilt, sen par)

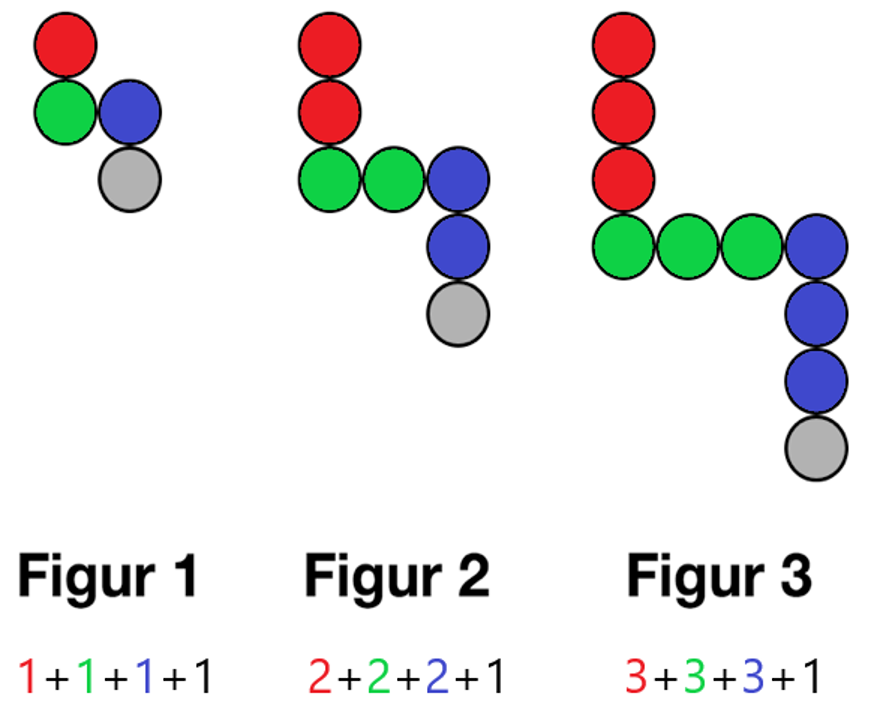
1. 2•n+n+n
2. n+n+n+1
3. 3n+1
4. n+1
5. Vet inte

Vad?

Att utveckla förståelse för hur det går att hitta struktur (n som en enhet i figuren) i en figurs uppbyggnad och hur det går att använda den strukturen för att konstruera generella uttryck för ett mönster.

Hur?

Eleverna tänker först enskilt, sen diskussion med kamrat, sen röstar de. Efter röstning, Tryck på How´d we do för att visa röstresultat. Följ upp i helklassdiskussion där eleverna tydliggör sina resonemang på tavlan.

Du kan använda följande frågor för att stimulera elevernas undersökande samtal kring mönstren i helklass:

• Varför inte a? eller Varför inte d? Om det är ett alternativ som få eller ingen har valt.
• Hur ser du n i figuren? Kom fram och rita på tavlan.
• Många har valt antingen b eller c, på vilka sätt är de lika och hur skiljer de sig åt?

Varför?

Vi vet att det är gynnsamt att betrakta figurens struktur i enheter om n för att konstruera algebraiska uttryck till mer avancerade mönster och talföljder. I diskussionen vill vi därför att de gör kopplingen mellan figurens nummer, uttrycket och figurens struktur. De olika färgsättningarna ska hjälpa till att sätta fokus på mönstrets struktur. Svarsalternativen är valda så det skapas förutsättningar för utforskande samtal kring hur samma uttryck kan se olika ut och kopplas olika till mönstrets struktur.

6. Bygg figur 5 i geogebra enligt Miriams förslag: 3n+1 (Par) https://www.geogebra.org/m/FdbFuqh3

Vad?

Att utveckla förståelse för hur det går att hitta struktur (n som en enhet i figuren) i en figurs uppbyggnad och hur det går att använda den strukturen för att konstruera generella uttryck för ett mönster.

Hur?

Eleverna bygger figur 5 tillsammans i geogebra. När eleverna är klara trycker de på klar. Låt åtminstone en grupp visa på tavlan hur de har tänkt och gjort.

Varför?

Du som lärare får en chans att se om merparten av eleverna har tolkat samtalet i uppgiften innan på samma sätt. I uppgift 5 så har de tolkat en fiktiv elevs resonemang, syftet i uppgift 6 ska eleverna omsätta den tolkningen i en egen konstruktion. Om inte eleverna har tolkat resonemanget i uppgift 5 på samma sätt så skapas en möjlighet att på nytt lyfta elevernas resonemang och undersöka hur n kan ses i figuren.

7. Tre andra lösningsförslag har presenterats, försök bygga figur 3 i geogebra utifrån hur du tror att eleverna har tänkt när de skapade sina uttryck. (Par) https://www.geogebra.org/m/FdbFuqh3
   1. n+(n+1)+n
   2. (n+1)+(n-1)+(n+1)
   3. 3(n+1)-2
   4. Ett eget förslag

Vad?

Att utveckla förståelse för hur det går att hitta struktur (n som en enhet i figuren) i en figurs uppbyggnad och hur det går att använda den strukturen för att konstruera generella uttryck för ett mönster.

Hur?

Eleverna bygger figur 3 i par. Följ upp med en helklassdiskussion där åtminstone ett förslag redovisas av elever vid tavlan och används till grund för ett undersökande samtal.

Varför?

Tanken här är att i slutet kunna visa flera lösningar vid sidan av varandra och få upp ögonen för att det är olika lösningar för samma mönster. Här finns möjlighet att visa att alla uttryck blir samma, men försök att behålla fokus på mönstren och färgläggningen.

Avslutning

En bra avslutning är att sammanfatta lektionen genom att leda eleverna mot diskussionen om vad färgläggningen är bra till. Ett tillfälle att introducera idén att det kan vara ett verktyg för problemlösning i fall där vi inte i förhand vet hur det algebraiska uttrycket ser ut. En viktig princip som ni arbetat med är också att gå ifrån enklare (additivt) resonemang, där man utgår ifrån en startfigur och räknar uppåt till mer avancerade (multiplikativa) resonemang där man tar ökningen mellan två figurer flera gånger eller identifierar enheten n i figuren och multiplicerar med hur många gånger den upprepar sig.