Syfte och lärandeobjekt
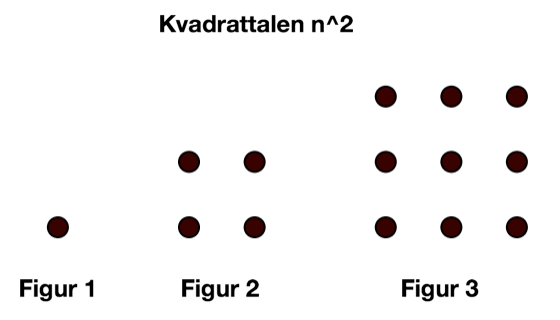
Syftet med lektionen är att tillsammans undersöka och komma till insikt om att olika sätt att se på n ger olika möjligheter när det kommer till att skriva algebraiska uttryck. Speciellt att när n ses som ökningen så begränsas man till att kunna skriva uttryck för aritmetiska mönster, dvs mönster med konstanta ökningar, men när n ses som en enhet i varje figur så blir det möjligt att även skriva uttryck för mönster med andra typer av ökningar (exempelvis kvadratal n2, se bild).
Material
Förbered en padlet med formatet ”vägg”. Se länk för instruktion om hur man skapar och använder en padlet. Förbered dessutom två mönster med papper och penna, ett relativt enkelt aritmetiskt mönster, som t.ex. mönstret i föregående lektion. Förbered också kvadrattalen, figur 1 med 1 prick, figur 2 med 4 prickar och figur 3 med 9 prickar, arrangerade i kvadrater (se bild ovan, fast utan rubriken som innehåller svaret).
Lektionsbeskrivning
Ni kommer att gå från rollen som konsumenter till att bli producenter av mönster för att upptäcka matematiska egenskaper hos mönster. En sådan egenskap är med vilken regel mönstret ökar, konstanta och icke-konstanta ökningar, som gör att olika metoder för att skriva algebraiska uttryck blir lämpliga. Eleverna skapar mönster som de sedan laddar upp i en padlet där alla kan se dem. Genom att uppmana till kreativitet och producera egna mönster så skapas utrymme för eleverna att blicka in i och skapa undersökande samtal kring strukturen i ett mönster.
Introduktion
Förslag på formuleringar för att inleda lektionen:
Vi ska idag fortsätta arbeta med mönster och utveckla verktyg för att beskriva mönster med algebraiska uttryck. Förra lektionen jobbade vi med detta mönstret (visa bild). Då såg vi att mönstret växte med en uppåt, en åt sidan och en nedåt (visa i bilden), vilket vi kunde beskriva med 3n+1 . Vi såg också att vi kunde hitta figurens nummer som enheter i mönstret, som t.ex. i figur 2 (visa i bild genom att ringa in 3st enheter om 2), vilket vi kunde beskriva med n3+1 .
Idag ska vi skapa egna mönster, och hjälpas åt att lösa varandras mönster. När ni har skapat ett eget mönster, och ett sätt att beskriva mönstret med ett algebraiskt uttryck, så ska ni ladda upp det med hjälp av datorn så att alla andra får en chans att lösa dessa.
Så nu ska ni i par, med papper och penna, skapa de tre första figurerna i ert mönster. Ni kan antingen börja med att rita ett mönster som ni sedan skriver ett uttryck till, eller så börjar ni med att skriva ett uttryck som ni sedan ritar ett mönster till.
Förslag på tidsdisponering i en 60min lektion: 10 min introduktion och instruktion, 20 min skapande (eller kortare om eleverna gått över till att lösa andras mönster), 15 min lösa andras mönster, 15 min (minst) helklassdiskussion.
Aktivitet
- Konstruera mönster
Vad?
Att utveckla förståelse för egenskaper hos mönster som gör det enklare eller svårare att skriva algebraiska uttryck samt motivera en fortsatt utveckling av metoden att leta n som en enhet i figuren.
Hur?
Eleverna arbetar i par med att skapa mönster och uttryck. De skriver sedan uttryck till varandras mönster allt eftersom de laddas upp i padleten.
När den första gruppen är klar att ladda upp sitt mönster pausar du elevaktiviteten och visar eleverna de olika alternativen för att ladda upp deras mönster, med hjälp av de två mönster du förberett (klicka här för instruktionsvideo för hur du laddar upp mönster i padlet). Om du sett att någon grupp är på väg att skapa det kvadratiska mönstret så laddar du endast upp ditt enkla mönster, annars båda två. Uppmana snabba grupper att de får ladda upp mer än ett mönster om de vill.
Påtala för eleverna att de endast laddar upp sitt mönster, och inte avslöjar det tillhörande uttrycket.
Tipsa elever som har svårt att komma igång att skapa mönster att först skriva ett uttryck, eller att du hjälper dem skriva ett uttryck som de kan rita ett mönster till.
Varför?
Ett steg i att undersöka och bekanta sig med matematiska egenskaper är att gå från att vara konsument till att bli en producent. Som producent av mönster behöver eleverna fundera över hur deras regel ska se ut och hur den grafiska representationen kan göra det lättare eller svårare för en utomstående att kunna skriva ett uttryck.
Att konstruera egna mönster har visat sig vara både utmanande och utvecklande för elever. Förutom att det erbjuder goda möjligheter till lärande i aktiviteten så ger det även elever en känsla av ägande, ansvar och handlingsutrymme i anslutande diskussion. Det skapas förutsättningar för att utveckla elevernas förmåga att delta i undersökande samtal i matematik då eleverna känner ett ansvar över den matematik som skapas i klassrummet.
- Skriva uttryck till varandras mönster
Vad?
Att träna och utmana elevers förmåga att skriva algebraiska uttryck
Hur?
Eleverna jobbar enskilt eller i par med papper och penna och försöker skriva uttryck till varandras mönster, som är uppladdade i den gemensamma padleten.
Gå runt och notera vilka mönster som har enklare och svårare karaktär. Kvadrattalen kan förutsättas vara ett mönster av svårare karaktär.
Varför?
Eleverna ska utveckla sin förmåga att urskilja med vilken regel olika mönster ökar och kan uttryckas algebraiskt. De ska också ges möjlighet att möta mönster som inte följer den typ av regelbundenhet som aritmetiska mönster har. Det ger en ingång till det följande undersökande samtalet i helklass samt uppgiften i lektion 3.
Du noterar vilka mönster som eleverna verkar anse är av enklare och svårare karaktär som underlag för den efterföljande helklassdiskussionen. Det ger dig möjlighet att fundera över vilka mönster som vore lämpliga att fokusera på, och hur man kan urskilja n som en enhet i dessa.
- Undersökande samtal om enkla och svåra mönster i helklass
Vad?
Att utveckla förståelse för att olika sätt att se på n ger olika möjligheter när det kommer till att skriva algebraiska uttryck. Speciellt att förstå hur n som en enhet i figuren blir ett användbart verktyg då det handlar om att skriva algebraiska uttryck för mönster som inte bara följer regeln för aritmetiska mönster.
Hur?
Ni ska nu avsluta lektionen genom att driva upp ett undersökande samtal kring några utav de mönster som eleverna arbetat med. Som startpunkt så väljer du ut ett mönster som eleverna verkat anse varit enkelt att skriva ett uttryck till, och mönstret kvadrattalen. Dessa två mönster blir sedan utgångspunkten i helklassdiskussionen.
Börja med det enklare mönstret för att få igång samtalen. Diskutera sedan kvadrattalen, som antagligen har upplevts som ett svårt mönster. Undersök vad det är som gör det mönstret svårare än andra, t.ex. genom att be eleverna formulera en regel för ökningen med ord. Försöka att inte fastna i resonemangen, syftet är att få upp ögonen för dilemmat med icke-konstanta ökningar. Knyt sedan tillbaka till början, olika sätt att se n är olika gynnsamt här. Med den slutsatsen/vägledningen så ska eleverna försöka att gemensamt komma fram till ett uttryck.
Du kan använda följande frågor/uppmaningar för att stimulera elevernas undersökande samtal kring mönstren i helklass:
- Vad gjorde att ett mönster var svårare än ett annat?
- Testa att färglägga på olika vis för att lättare ta fram ett uttryck.
- Var ser ni n i mönstret? Uppmana eleverna att rita på tavlan
Varför?
Vi vill förbereda eleverna på att alla mönster inte är enkla aritmetiska talföljder med konstanta ökningar. Kvadrattalen är ett bra exempel på sådana där eleverna måste använda en annan metod. Basen*höjden kommer också att återkomma i lektion 3, så det är bra om alla har tagit del i inledande diskussion om hur det går att se i bilden och varför det fungerar på rektangulära figurer.
Avslutning
En bra avslutning är att sammanfatta vad som blivit slutsatserna i den avslutande helklassdiskussionen. Lyft fram kraften i matematik, att vi har enklare men begränsade metoder (identifiera ökningen) som fungerar i vissa fall men kanske inte i andra och att det finns lite mer avancerade metoder som hjälper i flera fall (som till exempel att identifiera n som en enhet). Passa på att även blicka framåt och berätta att ni kommer behöva dessa slutsatser från er diskussion om ni ska kunna lösa det problem som kommer i nästa lektion.
